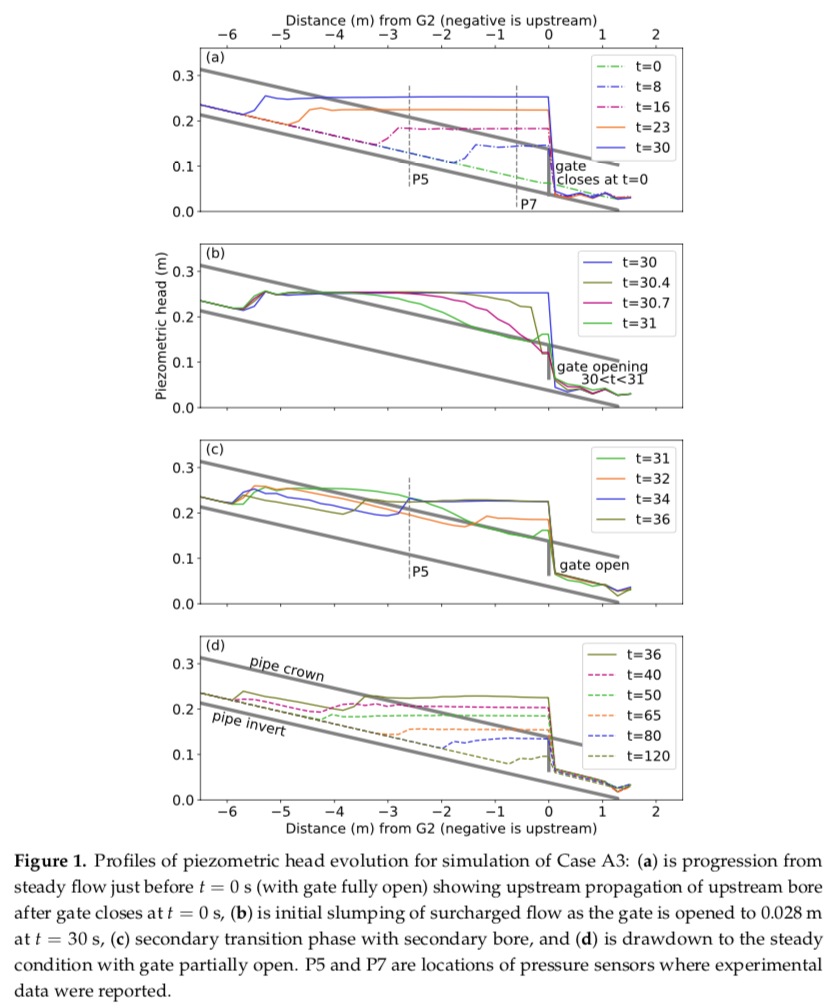
ABSTRACT: Piping systems (e.g., storm sewers) that transition between free-surface flow and surcharged flow are challenging to model in one-dimensional (1D) networks as the continuity equation changes from hyperbolic to elliptic as the water surface reaches the pipe ceiling. Previous network models are known to have poor mass conservation or unpredictable convergence behavior at such transitions. To address this problem, a new algorithm is developed for simulating unsteady 1D flow in closed conduits with both free-surface and surcharged flow. The shallow-water (hydrostatic) approximation is used as the governing equations. The artificial compressibility (AC) method is implemented as a dual-time-stepping discretization for a finite-volume solver with timescale interpolation used for face reconstruction. A new formulation for the AC celerity parameter is proposed such that the AC celerity matches the equivalent gravity wave speed for the local hydraulic head—which has some similarities to the classic Preissmann Slot used to approximate pressurized flow in conduits. The new approach allows the AC celerity to be set locally by the flow (i.e., non-uniform in space) and removes it as a free parameter of the AC solution method. The derivation of the AC method provides for only a minor change in the form of the solution equations when a computational element switches from free-surface to surcharged. The new solver is tested for both unsteady free-surface (supercritical, subcritical) and surcharged flow transitions in a circular pipe and is implemented in an open-source Python code available under the name “PipeAC.” The results are compared to laboratory experiments that include rapid flow changes due to opening/closing of gates. Results show that the new algorithm is satisfactory for 1D representation of unsteady transition behavior with two caveats: (i) sufficient grid resolution must be applied, and (ii) the shallow-water equation approximations (hydrostatic, single-fluid) limit the accuracy of the solution with regards to the celerity of the turbulent unsteady bore that propagates upstream. This research might benefit any piping network model that must smoothly handle unsteady transitions from free surface to surcharged flow.