Accuracy order of Crank-Nicolson discretization for hydrostatic free surface flow
ABSTRACT: Application of Crank–Nicolson (CN) discretization to the hydrostatic (or shallow-water) free-surface equation in two-dimensional or three-dimensional Reynolds-averaged Navier–Stokes models neglects a second order term. The neglected term is zero at steady state, so it does not appear in steady-state accuracy analyses. A new correction term is derived that restores second-order accuracy. The correction is significant when the amplitude of the surface oscillation is within two orders of magnitude of the water depth and the barotropic Courant–Friedrichs–Lewy (CFL) stability condition is less than unity. Analysis shows that the CN accuracy for an unforced free-surface oscillation is degraded to first order when the barotropic CFL stability condition is greater than unity, independent of whether or not the new correction term is applied. The results indicate that the semi-implicit Crank–Nicolson method, applied to the hydrostatic free-surface evolution equation, is only first-order accurate for the time and space scales typically used in lake, estuarine, and coastal ocean studies.
EXTRACT: Figure 3.
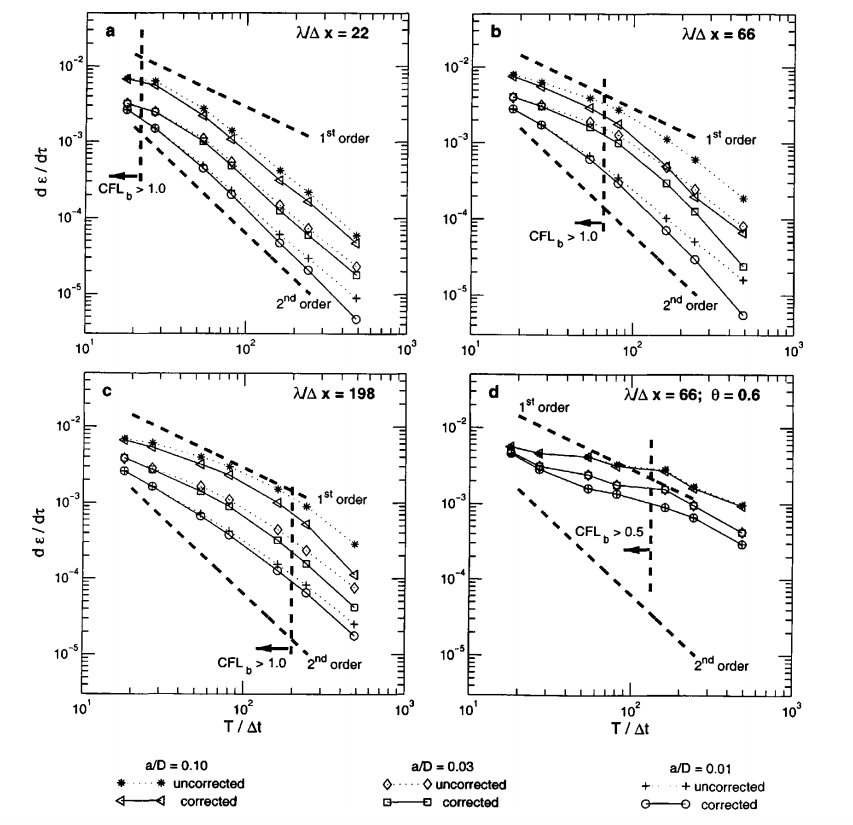
Fig. 3. Rate of root mean square error accumulation as time step is refined for simulation using Crank–Nicolson discretization with spatial resolutions of (a) 999×0.9 m; (b) 333×0.3 m; (c) 111×0.1 m; and using the theta method (d) with spatial resolution of 333×0.3 m.
