ABSTRACT: Three-dimensional hydrostatic models are often used to represent stratified dynamics and large-scale circulations in lakes and coastal oceans. However, non-linear internal wave evolution is fundamentally non-hydrostatic, so any hydrostatic model will eventually fail if non-hydrostatic effects accumulate. In this paper, we demonstrate that the time scale of baroclinic wave steepening provides a temporal horizon for model skill when sufficiently fine model grid scales are applied. At coarser grid scales, model results may be dominated by either diffusion or dissipation prior to the time scale of steepening. Methods for estimating numerical viscosity and diffusivity are developed, along with approximate predictive scales for the Centre for Water Research Estuary and Lake Computer Model (CWR-ELCOM). Results indicate that numerical diffusion of the pycnocline (i.e. thermocline or halocline) may rapidly increase past the time scale of steepening for a well-resolved model, and that somewhat coarser horizontal grid scales may be preferable for integrations beyond the time scale of steepening. While the present application and analyses are for a specific model, the methodology is developed in a general formulation and could be applied to other models for insight into error accumulation.

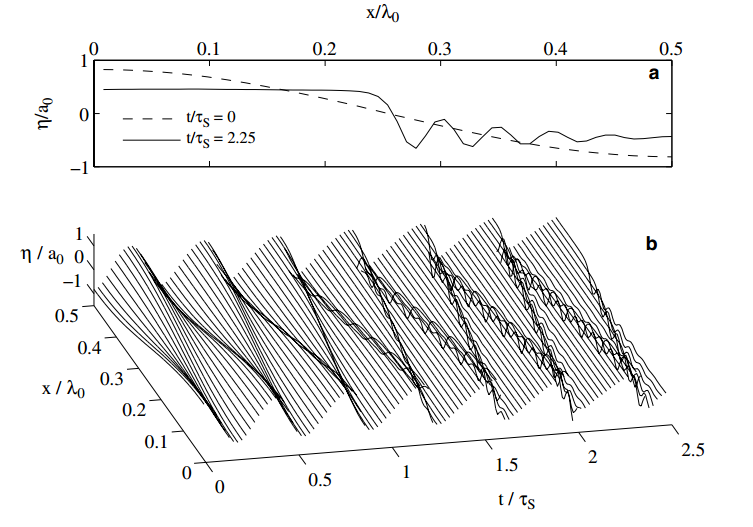
EXTRACT: Figure 3.

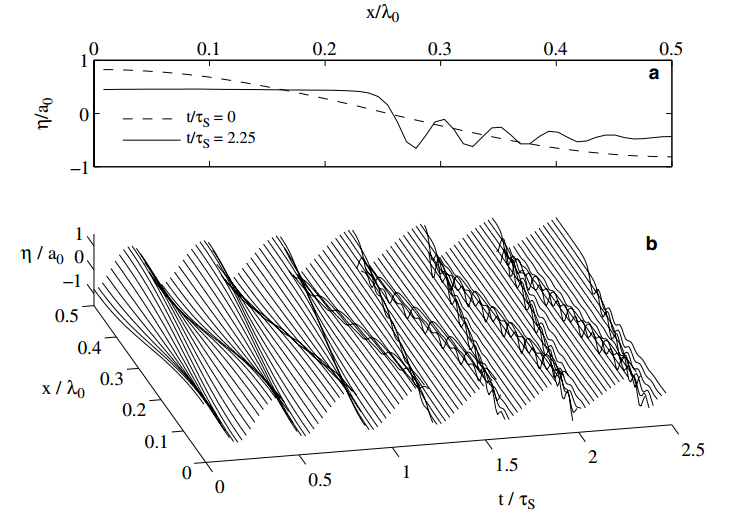
Fig. 3. Evolution of vertical displacement (g) of central isopycnal normalized by initial wave amplitude for (a) two discrete times and (b) for continuous time.