Time-centered split method for implicit discretization of unsteady advection problems
ABSTRACT: A new method for implicit solution of unsteady nonlinear advection equations is presented. This time-centered split (TCS) method uses a nested application of the midpoint rule to computationally decouple advection terms in a temporally second-order accurate time-marching discretization. The method requires solution of only two sets of linear equations without an outer iteration, and is theoretically applicable to quadratically nonlinear coupled equations for any number of variables. The TCS algorithm is compared to other nonlinear solution methods (local linearization, Picard iteration, and Newton iteration) and applied to the Crank-Nicolson discretization of the one-dimensional Burgers’ equation. The temporal accuracy and practical stability of the method is confirmed using an unsteady flow test case with an analytical solution. The method is shown to require computational effort similar to local linearization, but does not require discrete computation of a functional Jacobian for solution.
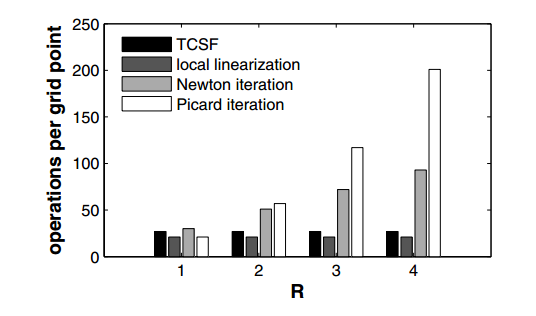
EXTRACT: Figure 4.
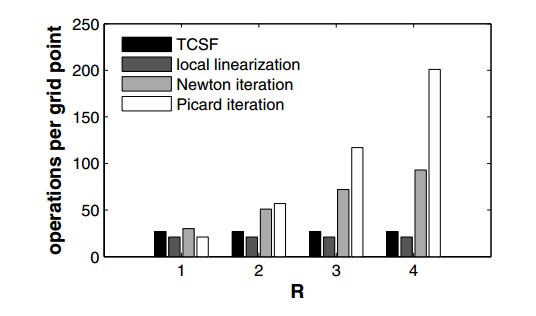
Fig. 4. Ideal operations per grid point for one time step using various nonlinear solution methods; R=number of outer iterations required for Newton convergence; it is assumed that the Picard method convergences in R^2 outer iterations