ABSTRACT: Basin-scale internal waves are inherently nonhydrostatic; however, they are frequently resolved features in three-dimensional hydrostatic lake and coastal ocean models. Comparison of hydrostatic and nonhydrostatic formulations of the Centre for Water Research Estuary and Lake Computer Model provides insight into the similarities and differences between these representations of internal waves. Comparisons to prior laboratory experiments are used to demonstrate the expected wave evolution. The hydrostatic model cannot replicate basin-scale wave degeneration into a solitary wave train, whereas a nonhydrostatic model does represent the downscaling of energy. However, the hydrostatic model produces a nonlinear traveling borelike feature that has similarities to the mean evolution of the nonhydrostatic wave.

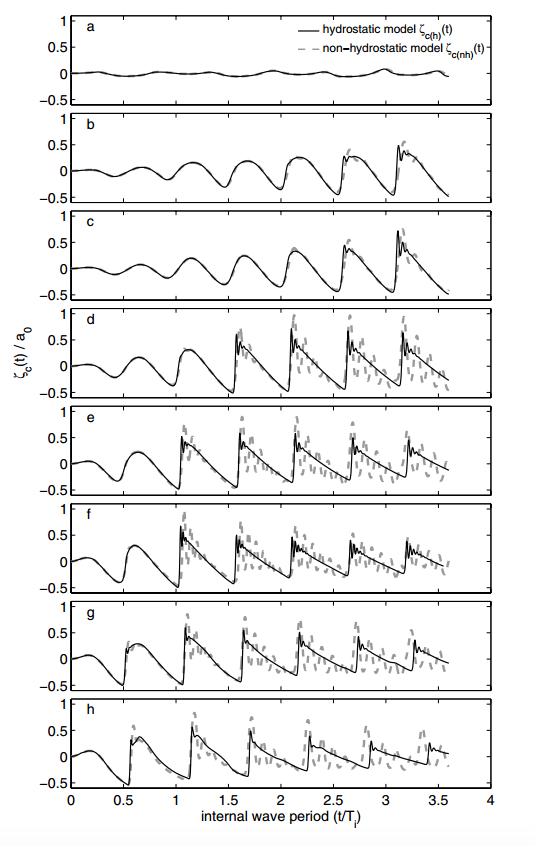
EXTRACT: Figure 6.

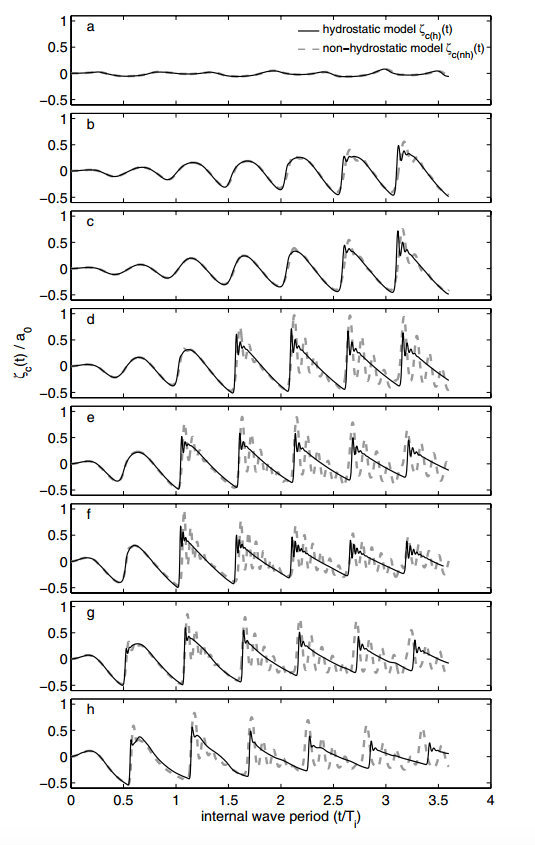
Fig. 6. Nonlinear wave evolution at standing wave node. Comparison for the nonhydrostatic and hydrostatic model isopycnal displacements at the central wave gauge normalized by the initial wave amplitude, \zeta_{C(nh)} (t)/a_0, and \zeta_{C(h)} (t)/a_0(t). Conditions for cases are presented in Table 1. Frame (a) represents a linear standing wave with no nodal oscillations. Nonlinearity of the experiments increases in successive frames of the figure.