ABSTRACT: New integral, finite-volume forms of the Saint-Venant equations for one-dimensional (1-D) open-channel flow are derived. The new equations are in the flux-gradient conservation form and transfer portions of both the hydrostatic pressure force and the gravitational force from the source term to the conservative flux term. This approach prevents irregular channel topography from creating an inherently non-smooth source term for momentum. The derivation introduces an analytical approximation of the free surface across a finite-volume element (e.g., linear, parabolic) with a weighting function for quadrature with bottom topography. This new free-surface/topography approach provides a single term that approximates the integrated piezometric pressure over a control volume that can be split between the source and the conservative flux terms without introducing new variables within the discretization. The resulting conservative finite-volume equations are written entirely in terms of flow rates, cross-sectional areas, and water surface elevations – without using the bottom slope (S₀). The new Saint- Venant equation form is (1) inherently conservative, as compared to non-conservative finite-difference forms, and (2) inherently well-balanced for irregular topography, as compared to conservative finite-volume forms using the Cunge–Liggett approach that rely on two integrations of topography. It is likely that this new equation form will be more tractable for large-scale simulations of river networks and urban drainage systems with highly variable topography as it ensures the inhomogeneous source term of the momentum conservation equation is Lipschitz smooth as long as the solution variables are smooth.

RESULTS:

We start with the traditional differential Cunge-Liggett form of the Saint Venant Equations (SVE), where momentum is

A conservative finite-volume C-L form (or variants) is typically preferred for solutions of the SVE in natural channels. We show that we can write a new finite-volume conservative form that has some significant advantages in the simplicity of the source term containing the free surface. Three different forms are presented as

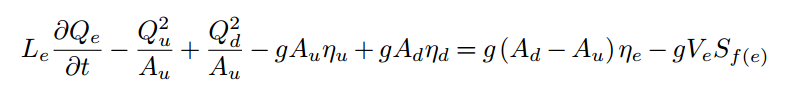
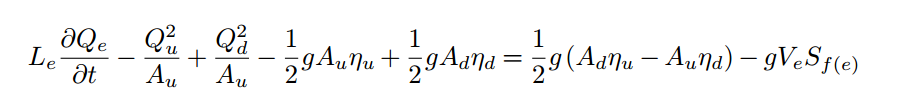
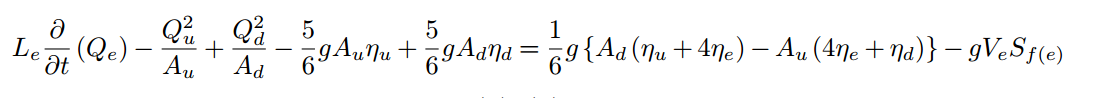
The above correspond to different approximations of the relationship between the spatially-varying bottom bathymetry and the free surface in the development of the discrete pressure term.  These terms occur because of the divergence/convergence of the free surface and bottom, e.g.

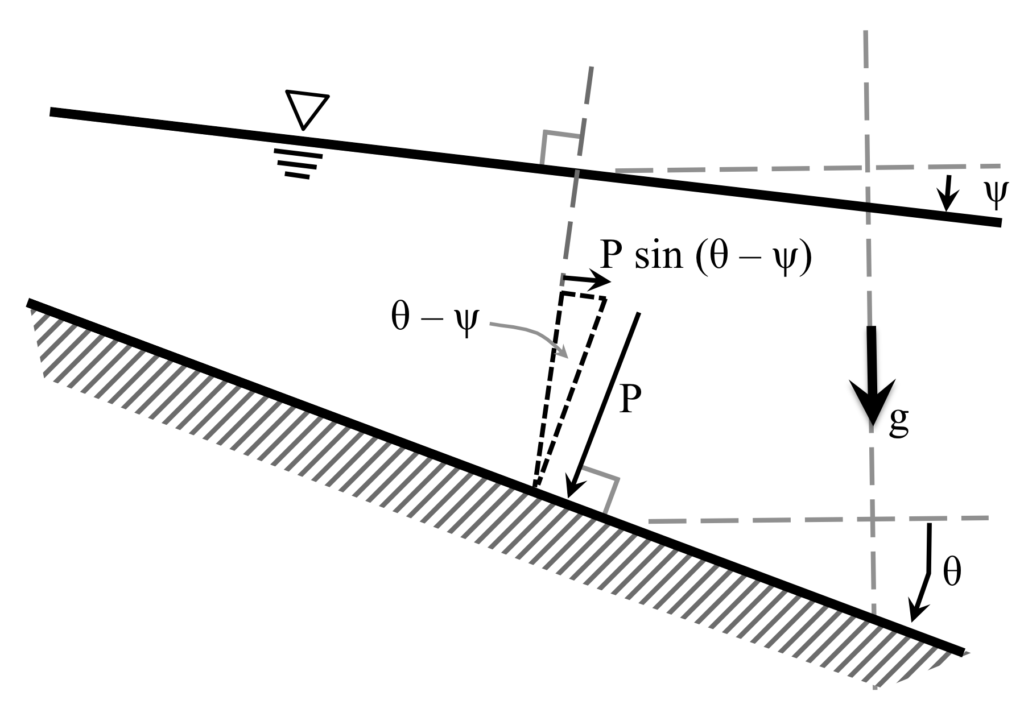
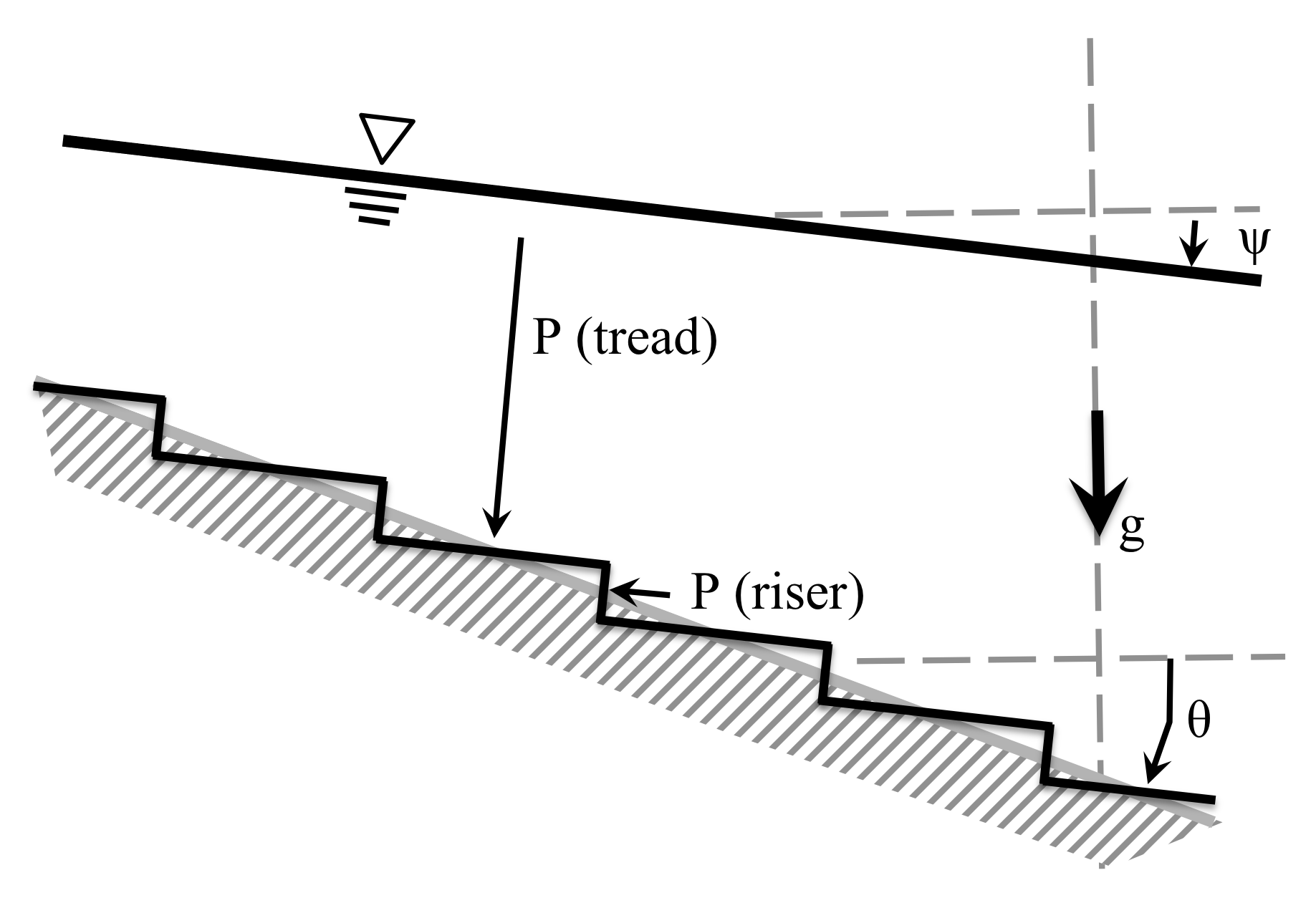
We can discretize the above by considering a stair-step bathymetry:

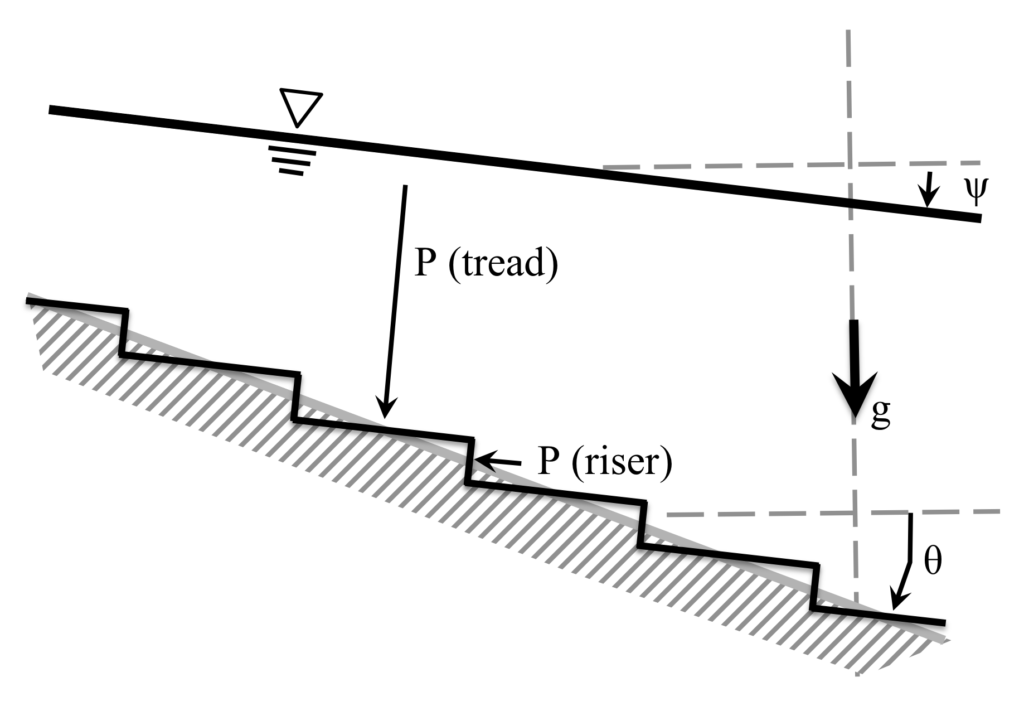
As the number of stair steps goes to infinity, we can represent the bottom pressure by an analytical function. Similarly, we can use an analytical function (e.g. linear slope) for the free surface. The quadrature of these functions provides the piezometric pressure contributions from the bottom that influence the finite volume.