ABSTRACT: Three-dimensional numerical models that solve the shallow water equations on a coarse fixed-grid, are limited in their ability to predict internal wave evolution, by the cumulative effects of numerical diffusion. Numerical diffusion of the metalimnion alters the internal response of the basin, and precludes simulations on seasonal to annual time scales. The discrete solution of the equations of motion leads to unintentional smoothing of advected gradients, which irreversibly increases the thickness of the metalimnion. The hydrostatic approximation exacerbates numerical diffusion by steepening internal basin-scale waves due to nonlinear effects until limited by numerical diffusion and dissipation. This steepening enhances horizontal gradients at the wave front which increases numerical diffusion locally, leaving a diffused metalimnion in the wake of the wave front. A method for correcting the numerical diffusion of mass based on conservation of background potential energy is proposed.

EXTRACT: Figure 1.

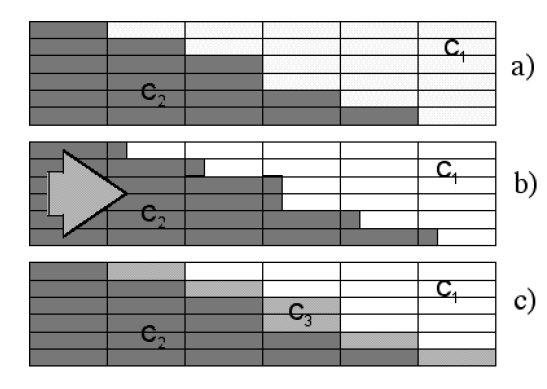
Figure 1: Schematic diagram of numerical diffusion. Consider two regions having property concentration c_1 and c_2, separated by a tilted interface that is sharply defined along the cell edges in a). Horizontal advection in b) introduces c_2 water in c_1 cells requiring spatial averaging due to the discrete grid, which results in water with property concentration c_3 in c).

ACKNOWLEDGMENTS: Supported by the Centre for Environmental Fluid Dynamics at the University of Western Australia, and by an International Postgraduate Scholarship.